弧度

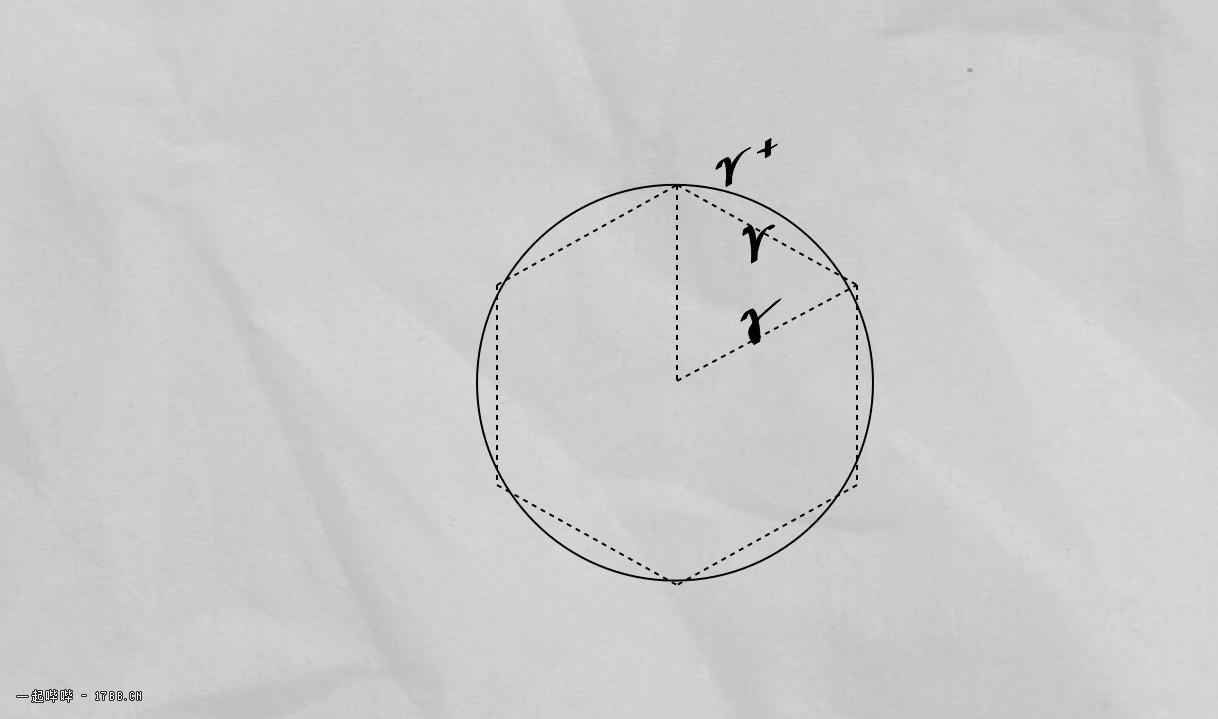
将半径r定义为内接六边形的边长，所分弧长设为r+，则周长实为6·r+，将“数”6r+（此时的6r+是一个数）分为（6r）+（6+）二部分，即r+里比r多出来的部分划归到（+），此时r+=（r）+（+）.

（6r）+（6+）=2·r［3+（3+/r）］，其中［3+（3+/r）］就是π

将2π消去，留下的就是1弧度，可以理解为圆是被“虚增的r”六分割的，［6r+（6+）］/2=［3r+（3+）］是平均虚增，提取r，［3+（3+/r）］是平均虚增系数也即π，这样任意半径R都有R·π=R［3+（3+/R）］，再乘回2是消除平均，得2πR，其中（3+/R）里的“+”是不能分割的成比例，因为它在构造上由完成的分割R取比例，也即其自身在比例上没有意义，这导致为消除它而构造的π没有比例意义

简言之，π就是消除［3+（3+/r）］