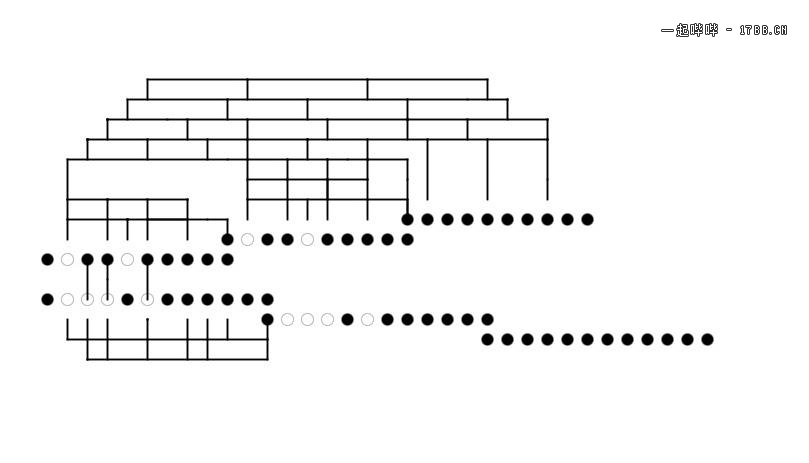
上面一排小点是10进制,11另起一行与10对齐,某种意义上代表前面的10个点重新作为1,但这里不考察这个属性,但认为11,12,…这一行本身保有123…属性,即12是本行的2
下面一排严格意义上是遵循同样规则的12进制,末端3位应该是AB10,但将12进制与10进制合并,使其成为10进制里12的倍数
在10进制里,第一行的10能够被2和5整除,认为这是相对于10进制第一层的乘法意义,在这个基础上,4,6,8成为2的倍数,就像认为第一因是2x5,各自的倍数比如4又成为4n的因
由于12能被2346整除,合并入10进制让第一x因变成2,3,4,5,6,提供了额外的可乘之机
又因为原本的计数规则里包含了重叠,10与11即是从头开始又是连续计位(这实际上就是集合与位相的范畴),所以上下二排合并不会有对齐意义,正如12第二行的2346会与10第二行错开而不重复第一行的对应
理解质数的关键在于理解我们一旦在数数的过程里有“除的意识”,这个构造的整体就会自动具备无限预除的性质,因为我们的除意识或者“计算能力”会自动识别所有的可乘因子,而这些因子的分布是累积性的,这就让所有能除的都在这样那样的除里,比如11,它实际上位于10的上面,2的倍数与5的倍数都会照顾到它,但这二个数承担10的第一x因,本来就是无限可除的集合,谁先谁后没有意义,只有算谁即谁,2x5=10,不是11,尽管排在10后面共享2和5的倍数,却不会体现出共享,因为不是在2x5的制约里排在10后面,反而是2x5属于无限互乘(可除)里失去制约意义下排在10后面,文字解释就到这里,能懂就会懂,不懂多说也没用
质数其实可以认为既有秘密也没秘密,如果认为有秘密,理解到这个程度差不多也理解了大半,可能是全部