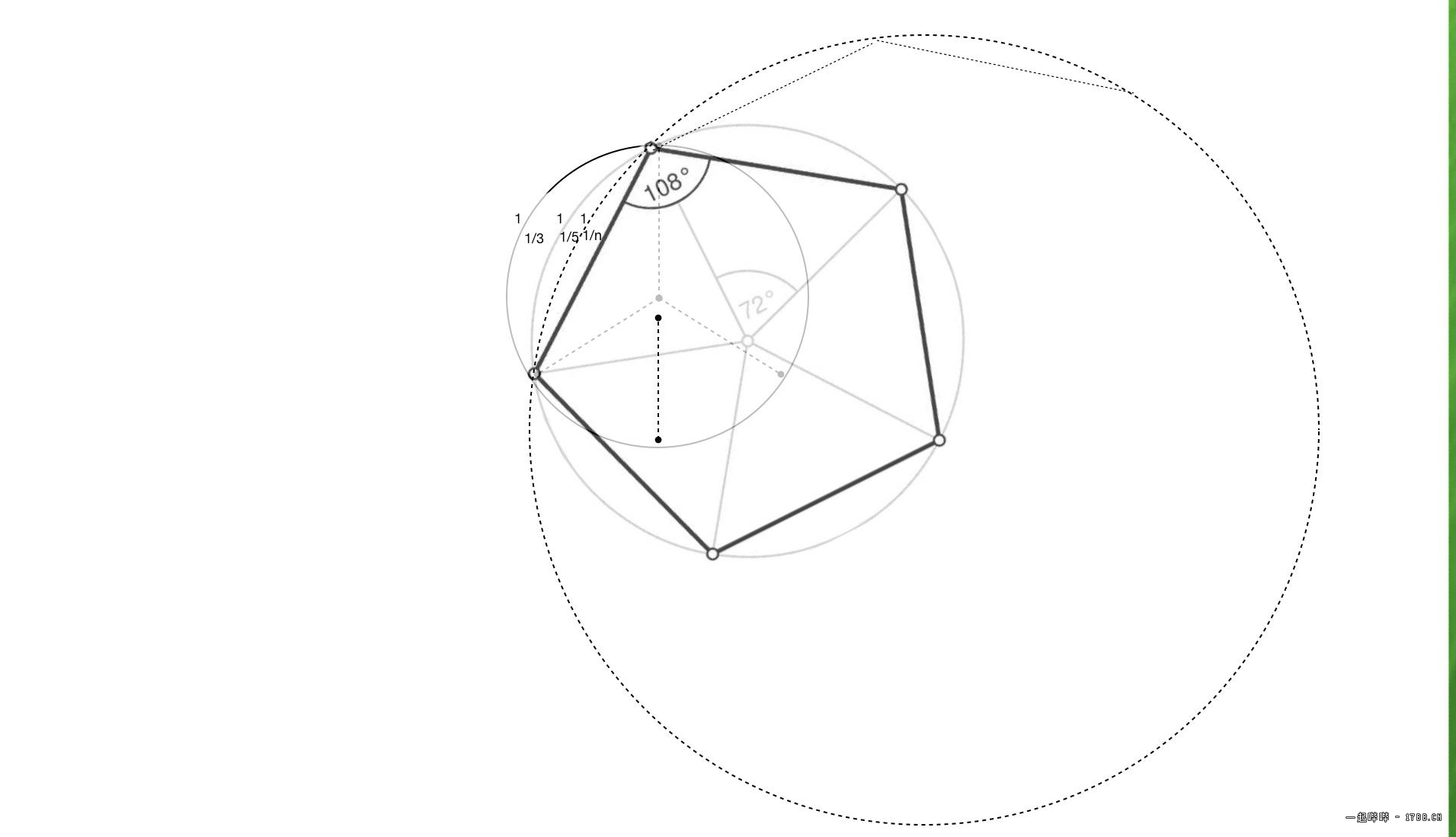
如图,弧长1不变,由1/3…1/n表达,n是整数,图是用奇数代表,圆周总是n,1/2可以嵌入1/3(3个1/2合并为一个1/3),1/1没有弧长意义(圆周未分割),这个通用模型的起点是1/3
圆周总是整数,意味半径永远不是整数,这是一种“给定”,就像去海边挖沙子,想得到100粒,给101粒,想得到50粒,给49粒,就是不刚好,这个比喻取“不刚好”的意思,101也是整数,并非用来比喻不能取整数,然而实际上,它有这个含义,不妨展开一下:100+π,π此时化身1,代表取整101附带精度意义,1的精度现在是1/π,取整100有个精度,这个精度可以寄托在取整101里,只要1的精度是1/π,1的精度是1/π可以直接用1取代π,这样100+π就转变为100+1,+-多少ppm,这样的例子比比皆是,收音机的频率稳定度,之类
给定基本上就代表没有例外,给定整数就找不到非整数,给定非整数就找不到整数
指定基于给定,上述通用模型给定非整数的半径,取整就是指定(给定整数取非整数就成为指定,指派)
指定是“上级取整”,比如现在流行 “云计算”,假设有5片云,从大到小,编上号,1…5“片”云,云本身没有“整数”意义,“片”有,所谓上级取整,就像把云放入看不见的盒子,这个盒子叫“片”,有5个盒子现在,取得整数5,而1/5,是对上级取整的引用,我们潜意识里会觉得1/n也是整数就是这个原因,此时代表格是“份”,5份1/5,5还是整数
引用上级取整会产生“概率”,1…5的云本来放在不同大小的盒子里,用1/5引用上级取整1…5时,每个盒子变成一样大(每个都是1/5),任何一个盒子都有1/5机会代表整体,20%
1/n总是包含1…n的平均,这是引用上级取整时代偿的“迭代”
既然是指定,就没有任何证明意义,不需要证明,也没办法证明,给定非整数,就会有与证明无关的取整(指定),如此,就指定1/3分割圆周3的半径为1好了,把这个圆“整个看作一片云”(当然也会有迭代的问题),也就是这个圆整个作为半径1,现在{圆周是3,1/3分割,弧长1,半径是个非整数},整体作为代表格,指定为半径1,如此,半径1/4就是把1/3变成1/12
这个1/3的圆,叠加了1/12的圆,弧长1,叠加了弧长1/4,由于这个叠加,弧长1得以成为半径1,弧长1/4得以成为半径1/4,而原本的非整半径,得以成为非整弧长,非整弧长有二个,一个从1/3来,一个从1/12来,反正是叠加的,这实际上是多重身份或多重性格的问题,用物理的方式描述:钮子和它的多次谐波
某个单元,之所以是个单元,因为它是个单元
某个单元,因为它是个单元,所以它是个单元
这是这个层次上的因果关系
某种意义上,话说到这里已经说明透了,因为因为就是因为,没必要再说什么,当然还是可以额外展开一些
“最初的”1/3与1/4叠加入1/12可以看成一种完成,或者说饱和,因为一个半径现在最大可以是1/12(上级取整12的引用),1/4圆已经在这里面了,看下其次的1/5圆,要借用这个一开始的指定取整取得自己的整半径,需要以3x5也即迭代入1/15的方式参与指定,其中1/12在半径里(最大)
这样,1/5的圆,最大的,有意义的取整半径的引用,是1/12,余1/3作为弧长与弧长1以及弧长1/5共享圆周5,而1/3是“最初的”,弧长1与弧长1/5的叠加好像根本不存在,也就是1/3与1/4叠加入1/12可以兼容1/15,1/5在这个兼容里,可有可无,说有吧,它以5个1/3的形式存在,说没有吧,一个1/3的圆把自己“本身”取整为半径1时,可以有1/12的引用,“自定义”的半径1可以引用为1/2…1/3…1/12,由于兼容1/15等同回归1/3,接下去就是闭环的重复利用了
整体上,属于通用模型里的“分形”