确定，不确定，否定

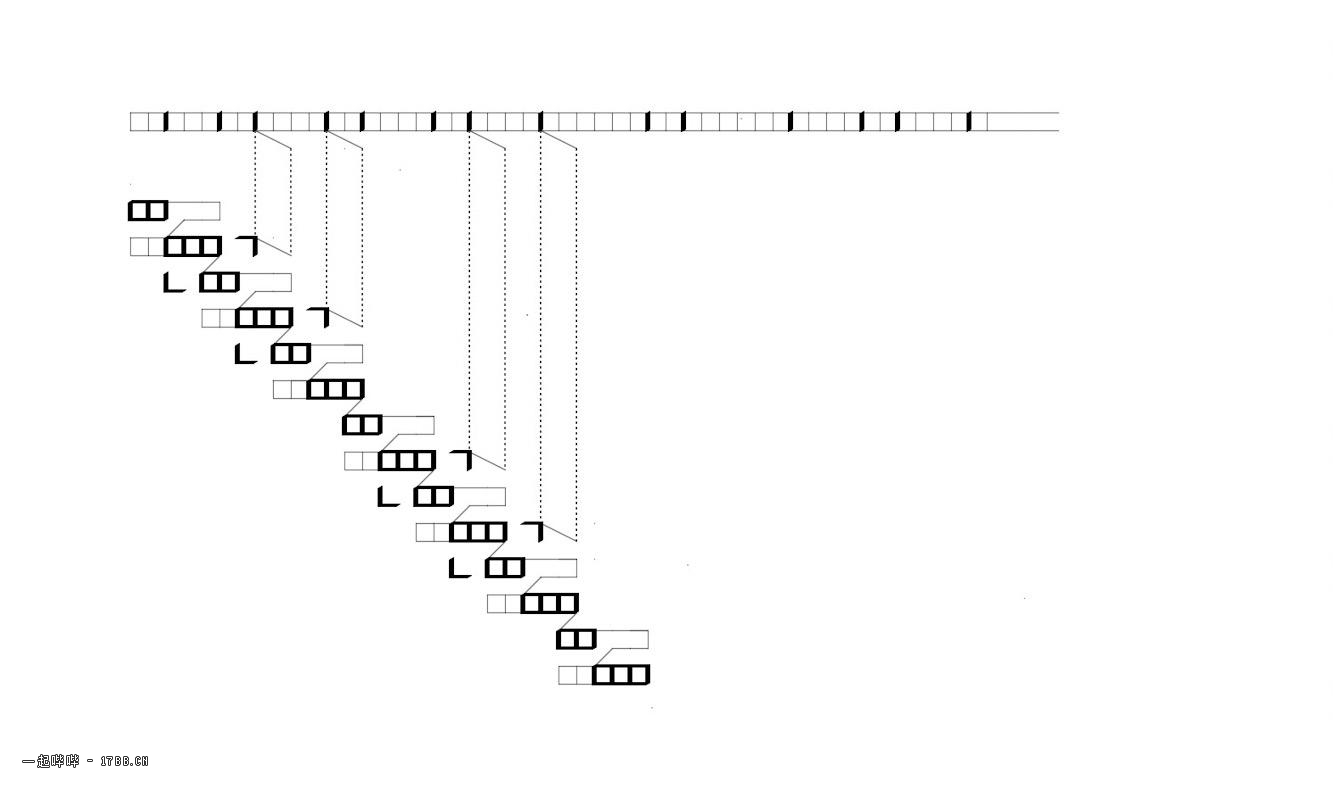
这张图是关于质数的，假设有这样一种关于确定与不确定的机制，认为1，2是确定的，3不确定，把3的不确定界定到3-5，这样数5就包括二个确定与一个包含变量3的不确定，（二+一）本身属于3，与不确定的内在（二个确定一个不确定）符合，把这个包含不确定的计数作为一个单元，比如说它是 “无”，无看起来就像“1，2，3，3，3”，现在反过来，数“无”5次，1，2是包含不确定的确定，3，4，5，基于这样一个逻辑：把3本身代表不确定看作3，4，5无法确定，用（3）=（3，4，5）表示，那么，重复3，3，3，并将这个重复当作3，4，5，那么，实际发生的过程就是（3，4，5），（3，4，5），（3，4，5）等同3，4，5，反正都有机会对，这样，不确定3，3，3就转化为确定3，4，5（那个什么重复1000遍），与1，2不同，数“无”5次以后，1，2是肯定不确定（包容）的确定，3，4，5是否认不确定（包含）的确定，但都是确定，如此完成一个迭代的计数单元，得到的确定数是1，2，3，4，5

就像揉面团一样，肯定之肯定，否定之否定，朋友的朋友的朋友的朋友…没完没了，但有一点，下一个迭代单元与上一个迭代单元至少要重叠1，这样就会出现5+4=9，+4=13，+4=17，+4=21…所以重复迭代应该出现的确定（每一代在自己看来都是得到确定的1，2，3，4，5，末位是5）都在奇数位

其实质数最难理解的就是它的飘忽不定，我们很难想象有什么机制可以产生不确定的确定，但我们最终还是能理解这些：分布即分组，否定即确定，浮现即否定，确定即肯定，某种意义上，出现在那里，已经是否定的结果，而这个否定本身，在出现的时候，不是以谁否定谁的方式出现，是一种已经完成了的确定出现，它就是那样，电池没电就是没电，一个确定的否定，所以回到这张图，我们实际上没有必要关注11从哪个位置移过来的，只是可以看起来从13移过来，结果上看起来这样而已，并不是原因，前面说过，得到的确定都在奇数位，现在因为有多重否定与肯定，因为迭代这还是容易理解的，只是无法知道具体的规则，“确定的得到发生位移”，这就像如果一个女的有几个男朋友…，总之位移只能出现在中间位，5+4=9是前面说过的，这里+4的中间位是+2，这样可以与前一个单元的包含不确定的确定3，4，5组成3+2的关系，又是一个5，反过来的确定1，确定2，确定3（3，4，5）确定4（确定3，4，5），确定5（确定3，4，5），而这个位移，会重新加入迭代，但不管怎么样，无非是在有间隔4（即间隔4相关）奇数位得到确定，在位移后新奇数位得到确定，保留“位移前”奇数位得到确定，放弃“位移前”奇数位得到确定，就是这四种情况，不会在偶数得到确定这件事本身将偶数区分出去了，位移的取舍又将奇数分为质数与非质数，从可控除确定的角度，偶数首先被排除，奇数有一部分在“不保留位移前奇数位得到的确定”这个分组里（即分布本身，分布同时也是分断）被排除，最后留下的都是不能被排除的确定，看起来就像除了被1和自己除不能被其它数除

总之就是面团揉久了熟了，迭代久了成了，成熟了